Illustrations
I very much enjoy making mathematical illustrations. Here are some examples. Created in MetaPost unless otherwise stated. Click image for PDF version.
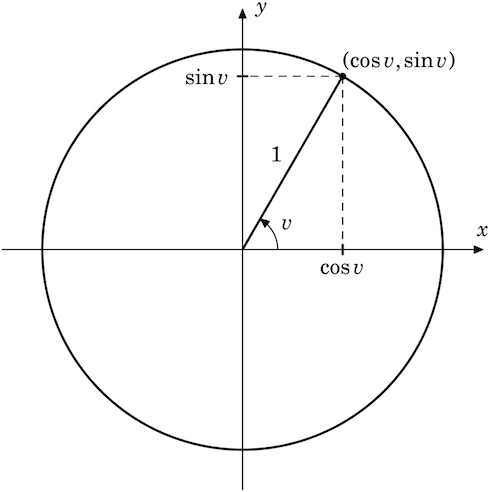
Trigonometric funtions. A simple illustration showing the definition of sine and cosine.

Differentiable function on a differentiable manifold.
A function f : M →
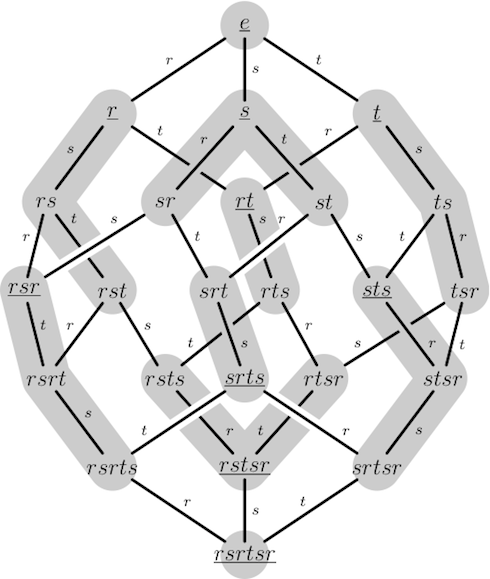
The right order of S4 with simple reflections r, s and t. The right cells are marked in grey, and the lines show what happens when multiplying an element with a simple reflection. The involutions are underlined. Created in Asymptote.
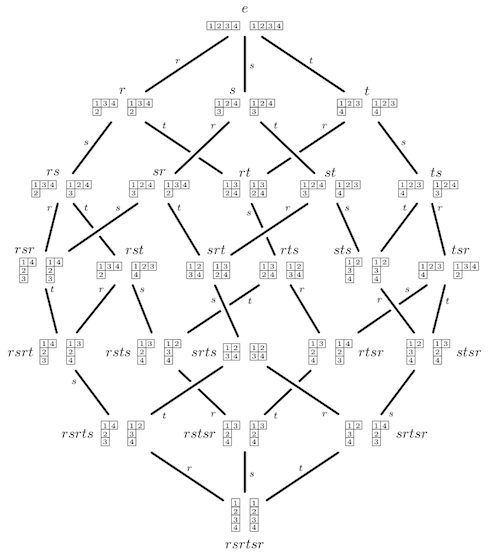
Robinson-Schensted correspondence. This image shows the pair of standard tableaux corresponding to each element of S4 under the Robinson-Schensted correspondence. Notice that the right cells in the previous picture are precisely the subsets sharing the same left tableaux.
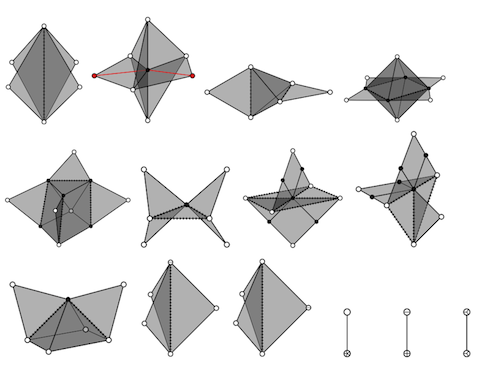
Prime six point metrics. These are the tight spans of all the prime metrics on six points. Each normal line has length 1 and each hashed line is a ‘diagonal’ of length 2. The white dots represent the points, the black dots are vertices in the tight span, and a white dot cut into sections represent points that are at the same place (i.e. the distance between them is zero) where each section represents an individual point. Created by writing raw PostScript code.
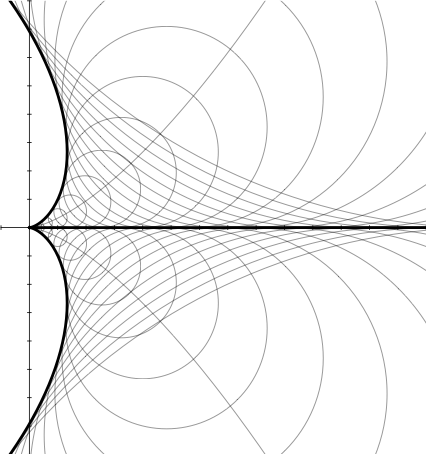
Envelope of a curve. The thick line is the envelope of the family of circles with center on the thin line with the same radius as the y-coordinate of the center.
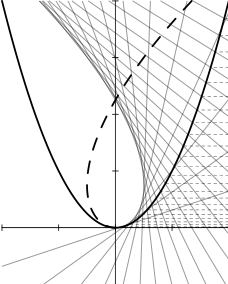
Catacaustic 1. The catacaustic of rays from a point at infinity reflecting in the curve y = x2.
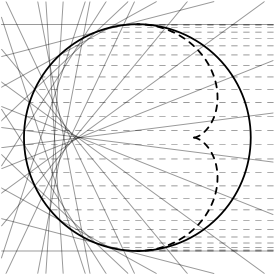
Catacaustic 2. The catacaustic of rays from a point at infinity reflecting in a circle, sometimes called the ‘coffe cup curve’.
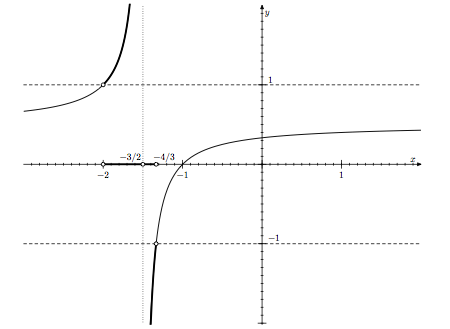
A graph. This is an image from the solution sheet of an exam I gave in basic mathematics for engineering students at Uppsala University. It illustrates the solution to the equation |(x+1)/(2x+3)| > 1.
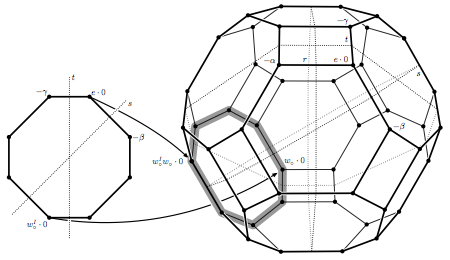
Parabolic inclusion. This is an image from my PhD thesis, illustrating a certain inclusion of B2 into B3. It shows the orbit of the zero weight under the dot action of the respective groups.
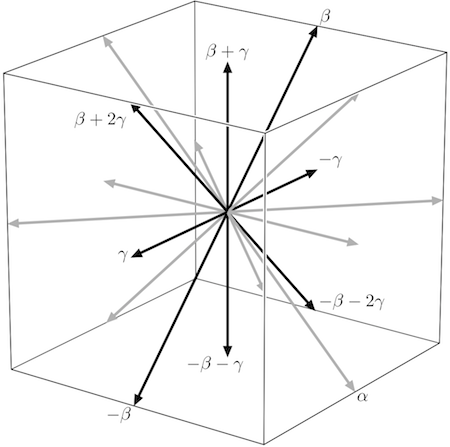
Root system. This is another image from my PhD thesis, which show the root system of type B3, with a sub root system of type B2 highlighted.
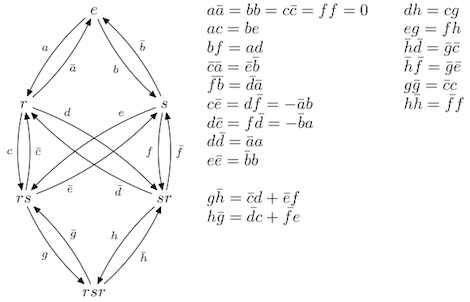
Category O as a quiver. A regular block of the Category O, type A2, as a quiver with relations. Adapted from Category O - Quivers and Endomorphism Rings of Projectives by Catharina Stroppel.
